|
A
fundamental question has long been if the number above can be
expressed by a simple numerical formula like a combination of elementary
values like π,
e and small numbers, or that it has a more arbitrary value based
on some underlying physical conditions.
Even
somebody like Feynman who was very well aware that the value
could change at higher energies kept on proposing the search
for such an expression (The Nobel Price won by Feynman was for
work in which vacuum polarization and charge renormalization,
issues responsible for the change of the constant at
extremely high energies, played an elementary role )
However,
the search for such an elementary formula has more or less been
given up nowadays. Proposed formulas generally needed six to
eight arbitrary numbers to get an eight to nine digit result and
don't look like anything seen in physics. The general consensus
is now that the constant is just some arbitrary number based on
underlying conditions.
Nevertheless,
such a formula, if found, may have far reaching consequences. It
would mean that the strength of the electro magnetic force in
its relation to other forces is in the limit determined by
geometry alone. This by itself would be one of the strongest
possible hints that the forces of nature are all coming from a
common physical source.
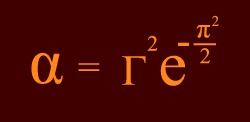
The
formula above generates the value of α
exact
in all ten known digits. The term gamma is a small correction on
the Gaussian exponential. It can be expressed as a
so-called radiative series in alpha. The series shows an elegant
simplicity:
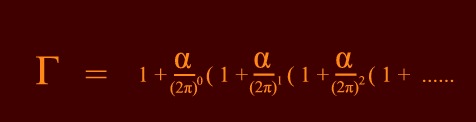
Expansion
as a function of
the powers of the coupling constant is a fundamental property of
all Field Theories where
a
term in αn
m
is generally described by an nth order Feynman Diagram.
Terms like 1
+ α
/ (2π)
remind us of the famous QED calculation of
the magnetic anomaly of the electron. This is the calculation
meant when people say that Quantum Mechanics is tested with the
highest precision of any physical theory. The
calculation for the magnetic moment starts of with the term 1
+ α
/ (2π)
as found
by Julius Schwinger in 1948.
|
